Binärzahlen: Der geheime Code der Computerwelt

Hättest du gedacht, dass alles, was du auf deinem Handy siehst, eigentlich nur aus Nullen und Einsen besteht? Ja, genau! Diese zwei kleinen Ziffern, die Grundlage der Binärdarstellung, sind die geheime Sprache der Computer. Wie funktioniert das eigentlich, dass aus so simplen Elementen komplexe Bilder, Videos und Texte entstehen können? Lass uns gemeinsam in die faszinierende Welt der Binärcodes eintauchen.
Die Darstellung von Zahlen im Binärsystem, auch Binärkodierung genannt, ist das Fundament der digitalen Welt. Im Gegensatz zu unserem gewohnten Dezimalsystem mit zehn Ziffern (0 bis 9) verwendet das Binärsystem nur zwei Ziffern: 0 und 1. Jede dieser Ziffern wird als Bit bezeichnet, die kleinste Informationseinheit in der Computerwelt. Durch die Kombination dieser Bits können wir jede beliebige Zahl darstellen.
Die Geschichte der Binärdarstellung reicht weit zurück. Schon im antiken China gab es Systeme, die auf dem Prinzip von zwei Zuständen basierten. Gottfried Wilhelm Leibniz, ein Universalgenie des 17. Jahrhunderts, formalisierte das Binärsystem und erkannte sein Potenzial für die Mathematik und die Logik. Im 20. Jahrhundert wurde die Binärdarstellung schließlich zur Grundlage der modernen Computertechnologie.
Die Bedeutung der Binärdarstellung liegt in ihrer Einfachheit und Effizienz. Computer arbeiten mit elektronischen Schaltungen, die zwei Zustände annehmen können: an oder aus, Strom fließt oder nicht. Diese Zustände lassen sich perfekt mit den Binärziffern 0 und 1 abbilden. Dadurch können Computer Informationen schnell und zuverlässig verarbeiten.
Ein Hauptproblem im Zusammenhang mit der Binärdarstellung ist die Länge der Zahlen. Große Zahlen benötigen im Binärsystem mehr Stellen als im Dezimalsystem. Dies kann zu Speicherproblemen führen. Es gibt jedoch verschiedene Techniken, um die Binärcodes zu komprimieren und den Speicherbedarf zu reduzieren.
Ein einfaches Beispiel: Die Dezimalzahl 5 wird im Binärsystem als 101 dargestellt. Wie kommt man darauf? Man teilt die Zahl immer wieder durch 2 und notiert den Rest. Die Reste, von unten nach oben gelesen, ergeben die Binärzahl.
Vorteile der Binärdarstellung sind die einfache Implementierung in Hardware, die hohe Fehlertoleranz und die klare Logik. Die beiden Zustände (0 und 1) lassen sich eindeutig unterscheiden, was Fehler minimiert.
Ein Aktionsplan zur Umsetzung von Binärzahlen in einem Projekt könnte die Definition der benötigten Datentypen, die Auswahl geeigneter Algorithmen und die Implementierung in der gewählten Programmiersprache umfassen.
Vor- und Nachteile der Binärdarstellung
| Vorteile | Nachteile |
|---|---|
| Einfache Implementierung in Hardware | Lange Zahlenketten für große Werte |
| Hohe Fehlertoleranz | Für Menschen weniger intuitiv lesbar |
| Klare Logik |
Häufig gestellte Fragen:
1. Was ist eine Binärzahl? - Eine Zahl, die nur aus 0 und 1 besteht.
2. Wie funktioniert die Umrechnung von Dezimal zu Binär? - Durch wiederholte Division durch 2.
3. Wo werden Binärzahlen verwendet? - In Computern und anderen digitalen Geräten.
4. Was ist ein Bit? - Die kleinste Informationseinheit (0 oder 1).
5. Was ist ein Byte? - Eine Gruppe von 8 Bits.
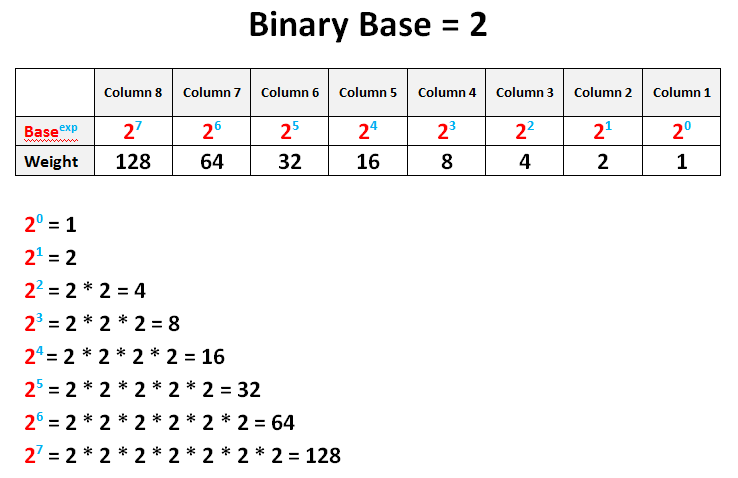
6. Wie rechnet man Binär zu Dezimal um? - Durch Multiplikation mit den entsprechenden Zweierpotenzen.
7. Warum sind Binärzahlen wichtig? - Sie bilden die Grundlage der digitalen Welt.
8. Was sind die Vorteile von Binärzahlen? - Einfache Implementierung, Fehlertoleranz, klare Logik.
Tipps und Tricks: Online-Konverter können die Umrechnung zwischen Dezimal und Binär erleichtern. Übung macht den Meister! Versuche, einfache Zahlen selbst umzurechnen.
Zusammenfassend lässt sich sagen, dass die Binärdarstellung von Zahlen, die Basis unserer digitalen Welt ist. Von Computern bis hin zu Smartphones, alles basiert auf diesem simplen System aus Nullen und Einsen. Obwohl die langen Zahlenketten für uns Menschen zunächst ungewohnt erscheinen mögen, bieten die Vorteile der Binärdarstellung in Bezug auf Hardware-Implementierung, Fehlertoleranz und Logik eine unschlagbare Grundlage für die digitale Technologie. Die Auseinandersetzung mit dem Binärsystem lohnt sich also, um die Funktionsweise unserer digitalen Welt besser zu verstehen. Vertiefen Sie Ihr Wissen und entdecken Sie die faszinierende Welt hinter den Nullen und Einsen! Beginnen Sie noch heute, die Sprache der Computer zu lernen!
Rot scheint die sonne text bedeutung und interpretation
Die spirituelle kraft der hymnen von guru nanak dev ji
Die geschichte hinter dem namen charcot marie tooth