Negative Zahlen meistern - Rechnen leicht gemacht

Minus mal Minus gleich Plus? Klingt verwirrend? Keine Sorge! Dieser Artikel taucht ein in die Welt der negativen Zahlen und erklärt die Regeln des Rechnens mit ihnen. Von einfachen Additionen bis hin zu komplexeren Multiplikationen – hier erfährst du alles, was du wissen musst.
Negative Zahlen begegnen uns im Alltag häufiger, als man denkt: Temperaturen unter dem Gefrierpunkt, Schulden auf dem Konto oder Stockwerke unter der Erde. Um diese Werte korrekt zu verarbeiten, ist das Verständnis der Rechenregeln für negative Zahlen unerlässlich. Wir erklären dir Schritt für Schritt, wie du mit diesen Zahlen umgehst und typische Fehler vermeidest.
Die Grundlagen des Rechnens mit negativen Zahlen sind essentiell für den Erfolg in Mathematik und vielen anderen Bereichen. Ob in der Schule, im Studium oder im Beruf – ein sicherer Umgang mit negativen Zahlen ist oft gefragt. Dieser Artikel bietet dir das nötige Wissen, um negative Zahlen souverän zu beherrschen.
Du fragst dich, wie du negative Zahlen addierst, subtrahierst, multiplizierst oder dividierst? Wir liefern dir klare Erklärungen und anschauliche Beispiele, die dir helfen, die Regeln zu verstehen und anzuwenden. Mit ein wenig Übung wirst du schnell zum Profi im Rechnen mit negativen Zahlen.
Dieser Artikel bietet dir einen umfassenden Überblick über die Mathematik mit negativen Zahlen. Von der Geschichte der negativen Zahlen bis hin zu praktischen Anwendungsbeispielen – hier findest du alles, was du brauchst, um dein Verständnis zu vertiefen und deine Rechenfähigkeiten zu verbessern.
Historisch gesehen hatten negative Zahlen lange Zeit einen schweren Stand. Sie wurden als "absurd" oder "fiktiv" abgetan. Erst im 17. Jahrhundert setzten sie sich endgültig durch. Heute sind sie ein unverzichtbarer Bestandteil der Mathematik.
Die Addition negativer Zahlen funktioniert ähnlich wie die Addition positiver Zahlen. Addiert man zwei negative Zahlen, so erhält man eine negative Zahl, deren Betrag der Summe der Beträge der beiden Zahlen entspricht. Beispiel: -5 + (-3) = -8. Subtrahiert man eine negative Zahl, so entspricht dies der Addition der positiven Gegenzahl. Beispiel: 5 - (-3) = 5 + 3 = 8.
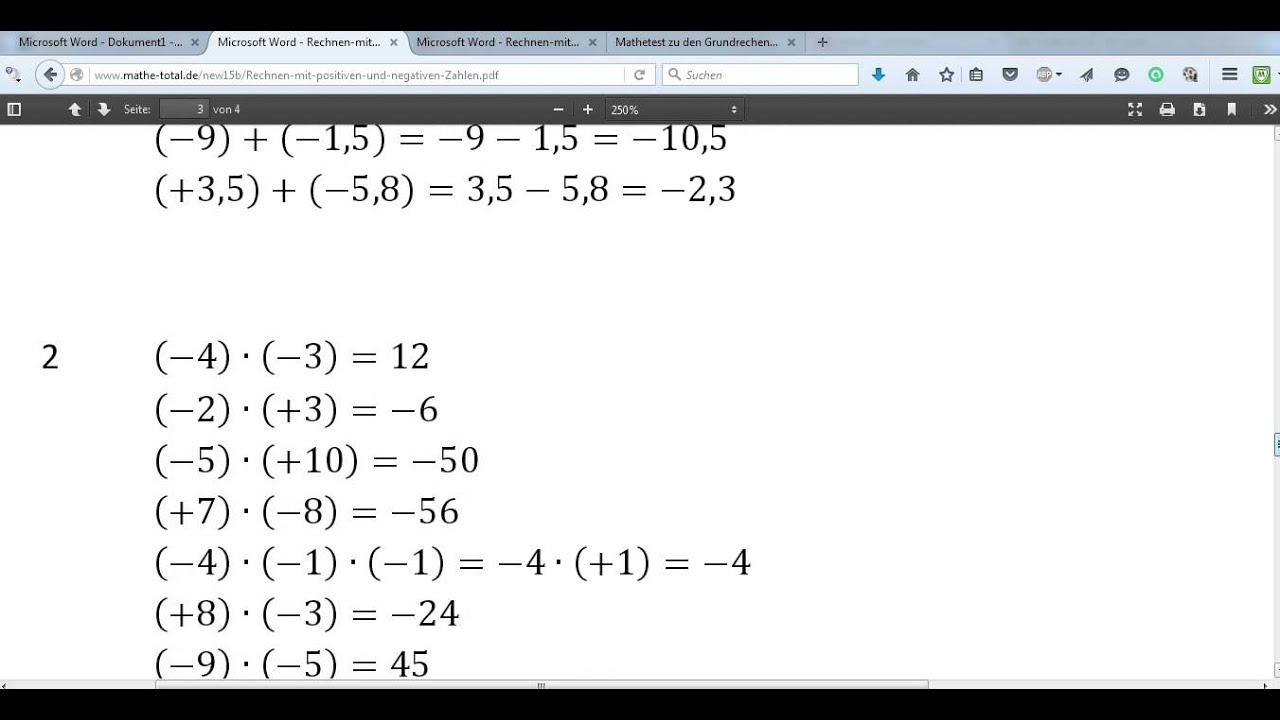
Bei der Multiplikation und Division zweier Zahlen mit unterschiedlichen Vorzeichen ist das Ergebnis immer negativ. Beispiel: -5 * 3 = -15 und 10 / (-2) = -5. Bei der Multiplikation und Division zweier negativer Zahlen ist das Ergebnis immer positiv. Beispiel: -5 * (-3) = 15 und -10 / (-2) = 5.
Vorteile: 1. Ermöglicht die Darstellung von Werten unter Null. 2. Vereinfacht Berechnungen in vielen Bereichen. 3. Eröffnet neue Möglichkeiten in der Mathematik und anderen Wissenschaften.
Aktionsplan: Übe regelmäßig mit Aufgaben unterschiedlicher Schwierigkeitsgrade. Nutze Online-Ressourcen und Lehrbücher, um dein Wissen zu vertiefen.
Häufig gestellte Fragen: 1. Was ist eine negative Zahl? 2. Wie addiere ich negative Zahlen? 3. Wie subtrahiere ich negative Zahlen? 4. Wie multipliziere ich negative Zahlen? 5. Wie dividiere ich negative Zahlen? 6. Wozu brauche ich negative Zahlen im Alltag? 7. Was ist der Unterschied zwischen einer negativen und einer positiven Zahl? 8. Gibt es Regeln für das Rechnen mit negativen Zahlen?
Tipps und Tricks: Verwende einen Zahlenstrahl, um dir die Rechenoperationen mit negativen Zahlen zu veranschaulichen. Denke daran, dass "Minus mal Minus" Plus ergibt.
Zusammenfassend lässt sich sagen, dass das Rechnen mit negativen Zahlen ein grundlegendes Konzept in der Mathematik ist, das für viele Bereiche des Lebens relevant ist. Von der Temperaturmessung bis hin zur Finanzbuchhaltung – negative Zahlen sind allgegenwärtig. Ein solides Verständnis der Rechenregeln ist daher unerlässlich. Nutze die hier vorgestellten Tipps und Tricks, um deine Fähigkeiten im Umgang mit negativen Zahlen zu verbessern und dich souverän in der Welt der Mathematik zu bewegen. Durch regelmäßiges Üben und das Verinnerlichen der grundlegenden Prinzipien kannst du Schwierigkeiten im Umgang mit negativen Zahlen überwinden und dein mathematisches Verständnis erweitern. Beginne noch heute damit, deine Kenntnisse zu vertiefen und profitiere von einem sicheren Umgang mit negativen Zahlen!
College football ranglisten bei espn ein familienblick
Mausnavigation auf zwei bildschirmen optimieren
Brauchen sie hilfe kontaktieren sie uns telefonisch